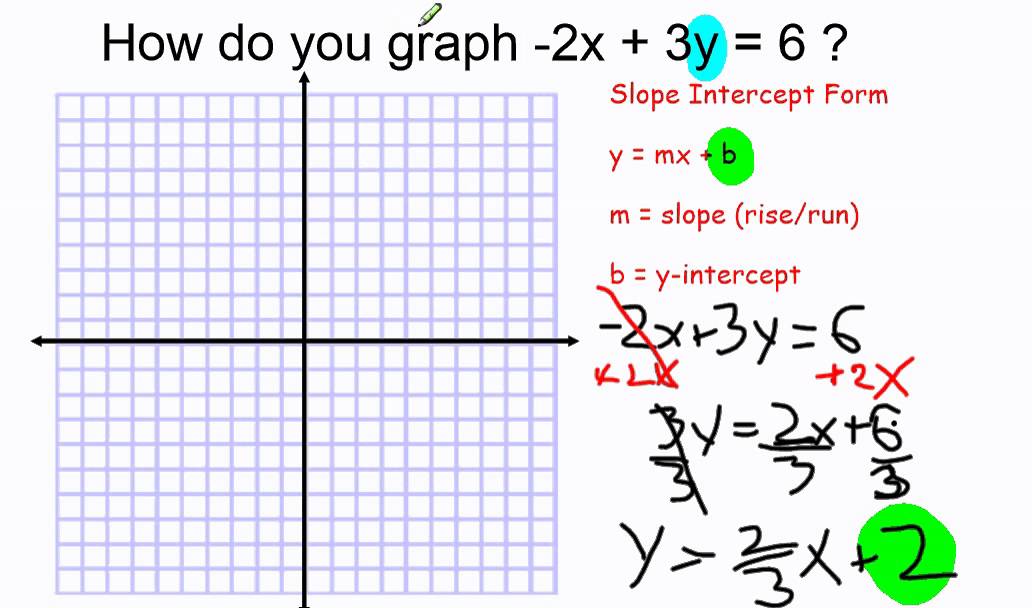
I actually solved this in my head No pencil, no paper But since you can't see into my head, let's put these equations in the form of y = mx b 2x y = 6 yields y = 2x 6 The y intercept is 6 The slope is 2, which makes the x intercept 32xy=6,2xy=2 To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 2xy=6 Choose one of the equations and solve it for x by isolating xWeegy 2x 5 = 4 2x 5 = 4 or 2x 5 = 4 2x 5 = 4;
Solve Graphically The System Of Linear Equations 4x 5y 16 0 And 2x Y 6 0 Determine The Vertices Of The Triangle Formed By These Lines And The X Axis Snapsolve
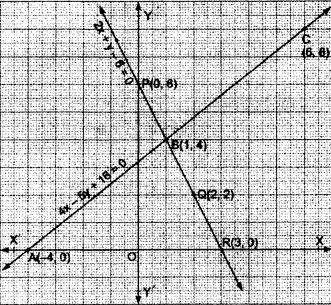
Solve graphically 2x+y=6 and 2x-y+2=0
Solve graphically 2x+y=6 and 2x-y+2=0- The system of equations are 2x y = 6 and x 2y = 2 Write the equations in slope intercept form y = mx b, where m is slope and b is y intercept The first equation is 2x y = 6 y = 2x 6 y = 2x 6 Compare the equation with slope intercept form y = mx b slope = 2 and y intercept is 6 y intercept is 6, so the line crosses the y axis at (0, 6)How to graph your problem Graph your problem using the following steps Type in your equation like y=2x1 (If you have a second equation use a semicolon like y=2x1 ;




Draw The Graph Of Thr Equation 2x 3y 6 0 Brainly In
2x = 4 5;Steps for Solving Linear Equation 2xy=6 2 x − y = 6 Subtract 2x from both sides Subtract 2 x from both sides y=62x − y = 6 − 2 x Divide both sides by 1 Divide both sides by − 1The Optimal Solution Is (2, 2) The Feasible Corner Points Are (0, 2), (0, 4), (2, 2) And
2xy=3 x2y=4 Answer by edjones(8007) (Show Source) Start with the given system of equations In order to graph these equations, we need to solve for y for each equation So let's solve for y on the first equation Start with the given equation Subtract from both sides Rearrange the equation Divide both sides by Break up the fraction for first line 2xy=6 point of intersection that is for x=0 y=6 and for y=0 x= 3 similarly for second line x2y2=0 point of intersection that is for x=0 y=1 and for y=0 x= 2 HENCE PLOT THE GRAPH Now the intersection comes at (2,2) by graph2(0) y = 6 y = 6 y = 6 The ordered pairs (3, 0) and (0, 6) are solutions of 2x y = 6 Graphing these points and connecting them with a straight line give us the graph of 2x y = 6 If the graph intersects the axes at or near the origin, the intercept method is not satisfactory
User y = 2x 3 2y = 4x 6 The system of equations has _____ solution(s) User For the following system, use the second equation to make a substitution for y in the first equationAnswer to Find an equation of the line that is tangent to the graph of f and parallel to the given line Function f(x) = 2x2 Line 2x y 2 = 02x = 4 5;
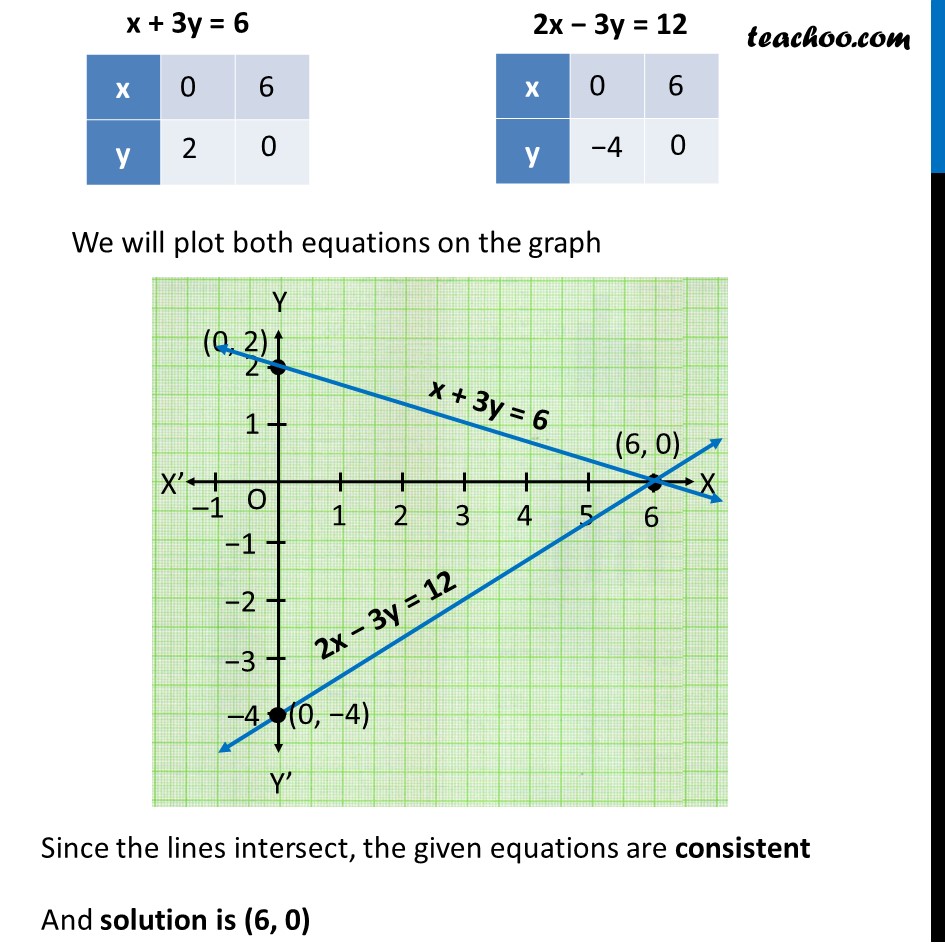



Example 4 Check Whether Equations X 3y 6 And 2x 3y



Solve The System Of Equation By Graphing 2x Y 6 X 2y 2 Mathskey Com
Solve Graphically 2x Y 6 And 4x 2y 4 0 Brainly In For more information and source, see on this link Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Youtube For more information and source, Solve It Graphically 1 X 2y 5 2x 3y 4 Brainly In For more information and source,Note You can also graph the system by rewriting the equations in slopeintercept form Thus, no matter what form the equations are in, all you need to do is graph them and identify the point of intersection It's Your Turn Now!Graphically, solve the following pair of equations 2xy=6 and 2xy2=0 Find the ratio of the areas of the two triangles formed by the lines representing thes




Q3d 3x Y 2 0 2x Y 8 Solve The Following Simultaneous Equation Graphically



Solved Graph Y 2x 3 6 Graph X 2 55 04 Unt Due 7 Chegg Com
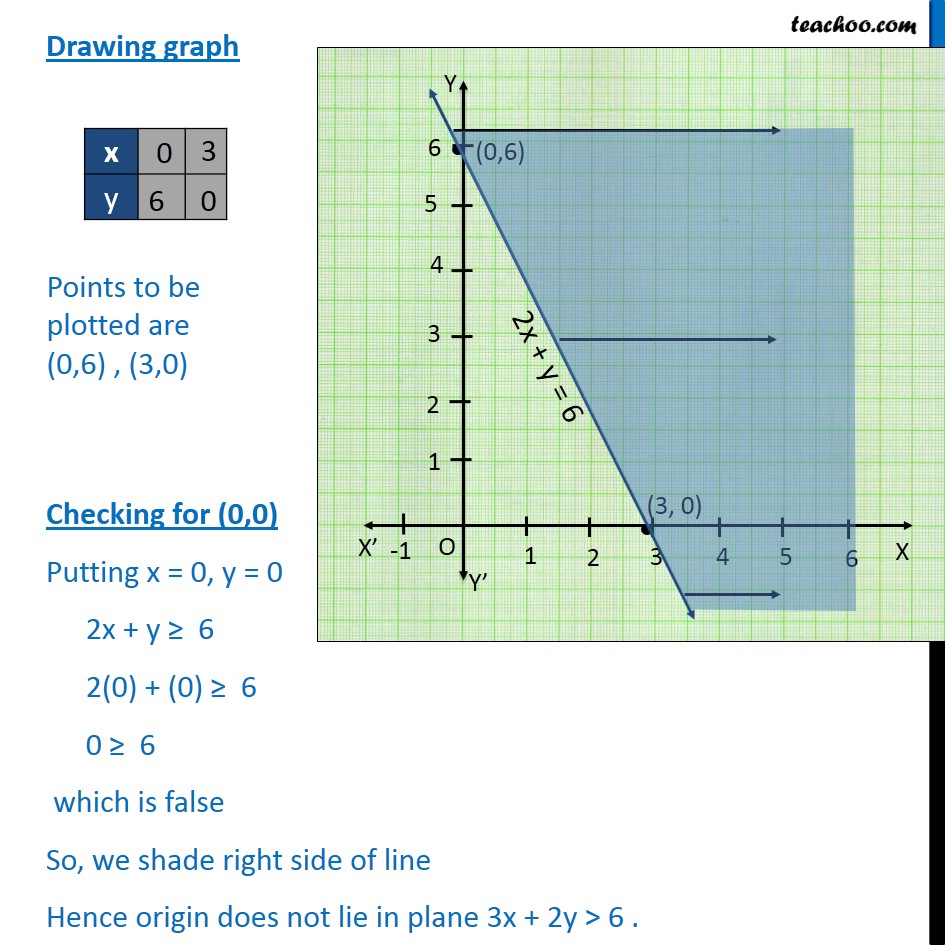
5xy= 6 thanks Answer by Edwin McCravy () ( Show Source ) You can put this solution on YOUR website!The Optimal Solution Is (0, 2) The Feasible Corner Points Are (0, 2), (0, 4), (2, 2) And (15, 15); Transcript Ex 63, 7 Solve the following system of inequalities graphically 2x y ≥ 8, x 2y ≥ 10 First we solve 2x y ≥ 8 Lets first draw graph of 2x y = 8 Putting x = 0 in (1) 2(0) y = 6 0 y = 6 y = 8 Putting y = 0 in (1) 2x (0) = 6 2x = 8 x = 8/2 x = 4 Points to be plotted are (0, 8), (4, 0) Drawing graph Checking for (0, 0) Putting x = 0, y = 0 2x y ≥ 8 0 ≥ 8 which




Ex 6 2 2 Solve 2x Y 6 Graphically Chapter 6 Class 11




Draw The Graphs Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Axis Find The Brainly In
Solve 2x y = −1 and y = −x3 4 graphically and check your solution Equation 1 xintercept = −12; Solve the following pair of linear equations graphically and shade the region bounded by these lines and x – axis; The inequalities are 2x 3y ≥ 6, x y ≥ 3 and y ≤ 2 Rewrite the inequalities so that solves for y , That's the slope intercept form and it will make the boundary line easier to graph 1) Draw the coordinate plane The first inequality 2x 3y ≥ 6 3y ≥ 2x 6 y ≥ ( 2/3)x 2 2) Graph the line y = ( 2/3)x 2 3) Since the inequality symbol is ≥ the boundary is




Draw The Graphs Of 2x Y 6 And 2x Y 2 0 Shade The Region B



Ex 6 2 2 Solve 2x Y 6 Graphically Chapter 6 Class 11
solve graphically 2xy=2&4xy=8 also find coordinates of the points where the lines meet axis x 2xy=6 and 2xy=2 solve by graphically The East West Social Survey organization surveyed 0 respondents from A Jinnah road Shops the weekly income of the respondents follows normal distr1 Graphically, solve the following pair of equations 2x y = 6 and 2x – y 2 = 0 Find the ratio of the areas of the two triangles formed by the lines rep



Graph 2x 3y 6 Youtube




1 Solve Graphically 2x Y 6 And 4x 2y 4 2 Solve Graphically 2x Y 2 And 4x Y 4 3 Solve Brainly In
2*xy(6)=0 Step 1 Equation of a Straight Line 11 Solve 2xy6 = 0 Tiger recognizes that we have here an equation of a straight line Such an equation is usually written y=mxb ("y=mxc" in the UK) "y=mxb" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axisGraph 2xy=6 2x − y = 6 2 x y = 6 Solve for y y Tap for more steps Subtract 2 x 2 x from both sides of the equation − y = 6 − 2 x y = 6 2 x Multiply each term in − y = 6 − 2 x y = 6 2 x by − 1 1 Tap for more steps Multiply each term in − y = 6 − 2 x y = 6 2 x by − 1 1Rearrange equations as y = 7 (2* x) and y = x 2 Plot the two functions for x = 0 to 5 in steps of 1 Read off the x value where the two lines cross In this example they cross with x = 3 and y = 1 So the solution is x=3 try values in original equ




Solve The Following System Of Linear Equations Graphically 2x Y 6 0 3x 2y 12 0 Please Give The Brainly In




Graphically Solve The Following Pair Of Equations 2x Y 6 And
See the answer Show transcribed image text Expert Answer 100% (1 rating) Solve the system of equations Equation 1 y=2x6 Equation 2 2xy=2 If Equation 2 is converted from standard form to slopeintercept form, you will see that both lines have the same slope, and are therefore parallel lines, and there is no solution Equation 2 2xy=2 Subtract 2x from both sides y=2x2 Divide both sides by 1 To solve such linear equations we should draw the graphs of these lines and point of intersection is the solution Let us draw graph of x −y = 2 As some points on the line are graph { (xy2) (x^2 (y2)^04) ( (x5)^2 (y7)^04) ( (x8)^2 (y6)^04)=0 , , 10, 10} Similarly, some points on 2x y = 6 are (0,6), (4, −2



Show Graphically That The System Of Equations 2x Y 6 6x 3y Is Inconsistent Mathematics Shaalaa Com




Solve Graphically 2x Y 2 0 4x Y 4 0
Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Youtube Ex 6 3 7 Solve 2x Y 8 X 2y 10 Graphically Ex 6 3 STEP 3 Similarly, we can find the xintercept and the yintercept of the graph of the equation y = x – 2 We get the xintercept as (0, –2) and the yintercept as (2, 0) STEP 4 Mark theClick here👆to get an answer to your question ️ Solve the following system of linear equations graphically 2x y = 6, x 2y 2 = 0 Find the vertices of the triangle formed by the above two lines and the x axis Also find the area of the triangleFirst, I have to find the xintercepts of the associated quadratic, because the intercepts are where y = x 2 – 3x 2 is equal to zero Graph xy=5 2x y > 3 x 1 Precalculus 9th grade




A 2x Y 6 0 B 4x 2y 4 0 Plot In Graph Plz Urgent Brainly In
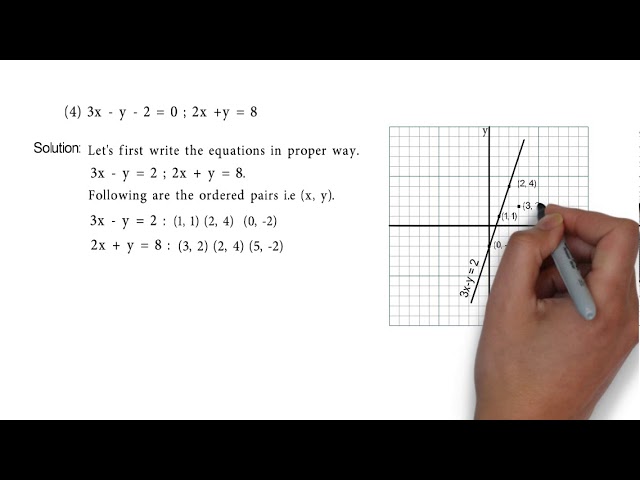



3x Y 2 0 And 2x Y 8 Problem Set 1 Q3 4 Of Linear Equations In Two Variables Algebra Youtube
User Solve the following system of equations graphically y 4 = 0 2x y 2 = 0 What is the solution set?Graphically, solve the following pair of equations2x y = 6 and 2x – y 2 = 0 Find the ratio of the areas of the two triangles formed by the lines representing these equations with the xaxis and the lines with the yaxis2 days ago Then count up or down the number of the y coordinate (up for positive, down for negative More Examples Solve x 2 – 3x 2 > 0;




1 Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Youtube




Ex 3 4 Q1 Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0
2x Y = 8 Maharashtra State Board SSC (English Medium) 10th Standard Board Exam Question Papers 238 Textbook Solutions Online Tests 39 Important Solutions 27 Question Bank Solutions 9046 Concept Notes & Videos 2232x y 2 = 0 asked in Linear Equations by Chandan01 ( 512k points)X = 1/2 or x = 9/2 User Given the following system of equations, identify the type of system x y = 4 x




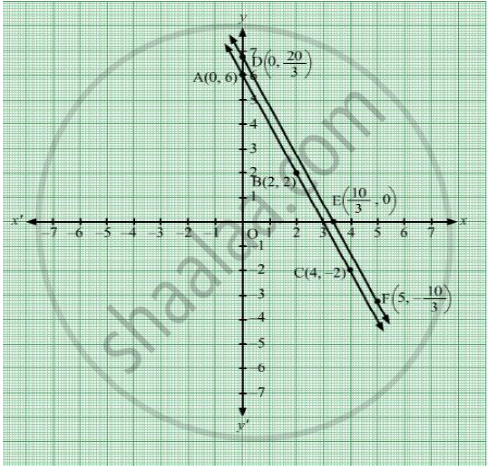
Draw The Graph Of The Following Pair Of Linear Equations X 3y 6 2x 312 Hence Find The Area Of Region Bounded By Lines X 0 Y 0 And 2x 3y 12




Solve Graphically 2x Y 6 And 4x 2y 4 0 Brainly In
Stepbystep explanation Im going to use GeoGebra for graphing the 2 lines I always find it helpful to move y to side of the equation and the rest of the equation to another side This is the slope intercept equation by the way We get our equations as y = 2x6 and y= 2x2 You can find that the common point is (2,2) between the lines searchQuestion Solve The Following System By Graphing 2x Y = 7 X2y = 6 This problem has been solved! Transcript Ex62, 2 Solve the given inequality graphically in twodimensional plane 2x y 6 2x y 6 Lets first draw graph of 2x y = 6 Drawing graph Checking for (0,0) Putting x = 0, y = 0 2x y 6 2(0) (0) 6 0 6 which is false So, we shade right side of line Hence origin does not lie in plane 3x 2y > 6




Solve The Following System Of Equations Graphically 2x 3y 6 0 2x 3y 18 0
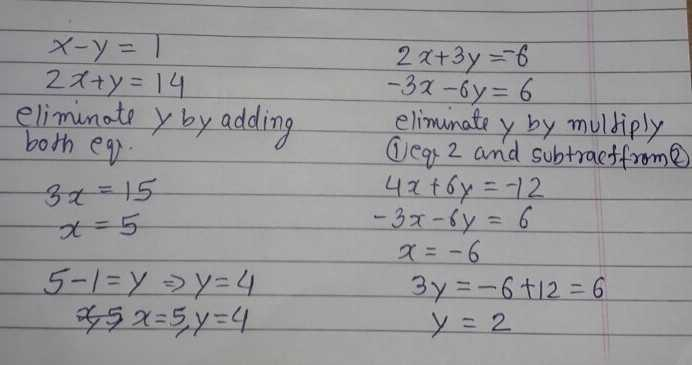



Solve Each System Algebraically Check Your Solution By Grap Scholr
Graphically, solve the following pair of equations 2x y = 6 2x – y 2 = 0 Find the ratio of the areas of the two triangles formed by the lines representing these equations with the xaxis and the lines with the yaxis2x y = 6; 6 Solve the following inequality graphically in two dimensional plane 2x – 3y > 6 Answer We draw the graph of 2x – 3y = 6 The line passes through (3, 0), (0, –2) AB represents the equation 2x – 3y = 6 Now consider the inequality 2x – 3y > 6 Putting x = 0, y = 0 0 = 0 > 6 is not true ∴ Origin does not lie in the region of 2x




Ex 6 3 3 Solve 2x Y 6 3x 4y 12 Graphically



Draw The Graph Of The Pair Of Equations 2x Y 4 And 2x Y 4 Studyrankersonline
Solve graphically the system of equations x – 2y 2 = 0 2x y – 6 = 0 Find the coordinates of the vertices of the triangle formed by these two lines and the xaxisWe draw the graph of line 2x y = 6x 0 3y 6 0Now, we consider a point O(0, 0), ie, originSubstitute in inequality 2x y ≥ 6, ie 7, 2(0) 0 ≥ 6 or 0 ≥ 6 which is not true∴ we mark that region which does not contain originNow, we draw the graph of line 3x 4y = 12x 0 4y 3 0Now, we consider a point O(0, 0), ie, originSubstituting in given inequality, 3x 4y ≤ 12, we2x 5 = 4;
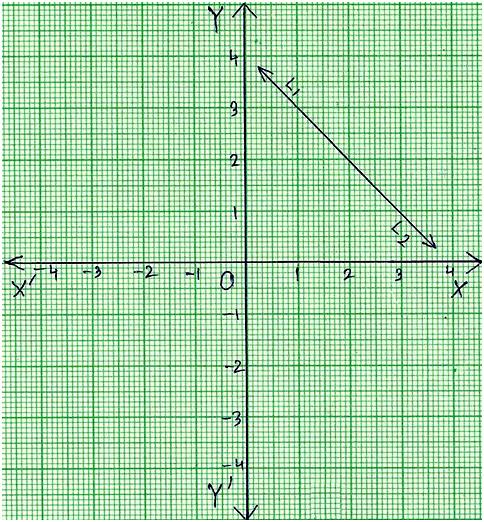



Simultaneous Equations Graphically Solve Graphically The System Of Equations



How To Solve 2x 3y 6 Quora
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 2xy=6;2xy2=0 Tiger Algebra Solver2xy = 8 5xy = 6 We get some points on each To get some points on 2xy = 8 We arbitrarily choose x=0 2xy = 8 2 (0)y = 8 0y = 8 y = 8 So one point is (0,8) We arbitrarily choose y=0 2xy = 8 2x0 = 8 2x = 8 x = 4 So oneY < 2 x − 6 y < 2 x 6 Use the slopeintercept form to find the slope and yintercept Tap for more steps Find the values of m m and b b using the form y = m x b y = m x b m = 2 m = 2 b = − 6 b = 6 The slope of the line is the value of m m, and the yintercept is the value of b b Slope 2 2




Solve The Following System Of Equations Graphically 4x 5y 16 0 2x Y 6 Determine The Brainly In
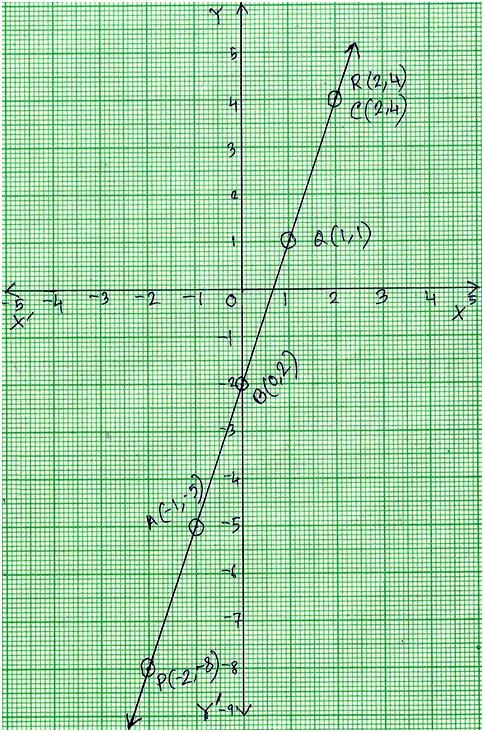



Simultaneous Equations Graphically Solve Graphically The System Of Equations
x y 6 = 0 x y = 0 What is the solution of the system?Y=x3) Press Calculate it to graph!Question Min 2x Y St X Y = 6 X = 0 Solve This LP Graphically And Choose The Correct Statement The Feasible Corner Points Are (0, 2), (0, 4), (2, 2) And (15, 15);




2x Y 6 0 4x 2y 4 0 Solve By Substitution Elimination And Graph Maths Pair Of Linear Equations In Two Variables Meritnation Com




Graphically Solve The Following Pair Of Linear Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Brainly In
Graphically, solve the following pair of equations 2x y = 6 2x – y 2 = 0 Find the ratio of the areas of the two triangles formed by the lines representing these equations with the xaxis and the lines with the yaxis Share with your friends Share 1 Here is the link for the similar answer to your querySolve the Following Simultaneous Equation Graphically3x – Y – 2 = 0 ;1Graphically, solve the following pair of equations 2x y = 6 and 2x y 2 Find the ratio of the areas of the two triangles formed by the lines representing these equations with the Xaxis and the lines with the Yaxis Ans 41 2Determine graphically, the vertices of the triangle formed by the lines y =3, x = 3y, and x y = 8
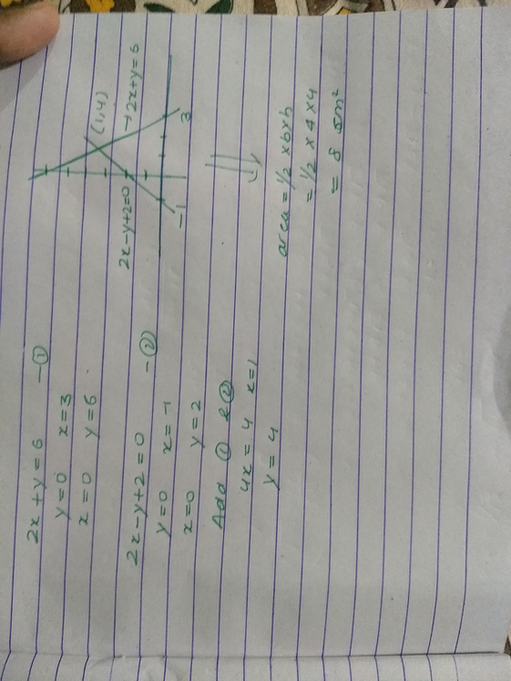



Draw The Graphs Of The Lines 2x Ty 6 And 2x Y 2 0 Shade The Scholr




Solve Graphically The System Of Linear Equations 4x 5y 16 0 And 2x Y 6 0 Determine The Vertices Of The Triangle Formed By These Lines And The X Axis Snapsolve
Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes 2x2=y2nd equation now write x an below that y and take a number and write it as x and with that no take first equation and like that take 2 more numbers and do the same thing with 2nd equation simultaneous equation 2xy=10 2xy=2 now cancel y and y and then add 2x and 2xthen add 10 and 2 which will be seen asClick here👆to get an answer to your question ️ Graphically , solve the following pair of equations 2x y = 6 and 2x y 2 = 0 find the ratio of the areas of the two triangles formed by the lines representing these equations with equations with the x axis and the lines with the y axis
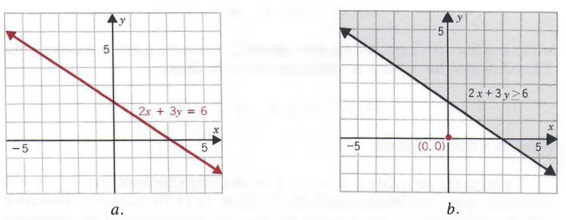



Graph Graph Equations With Step By Step Math Problem Solver
.png)



Solve The System Of Equations Graphically 2x 3y 6 0 2x 3y Maths Pair Of Linear Equations In Two Variables Meritnation Com




The Graph Of The Linear Equation 2x 3y 6 Is A Line Which Meets The X Axis At The Point Youtube
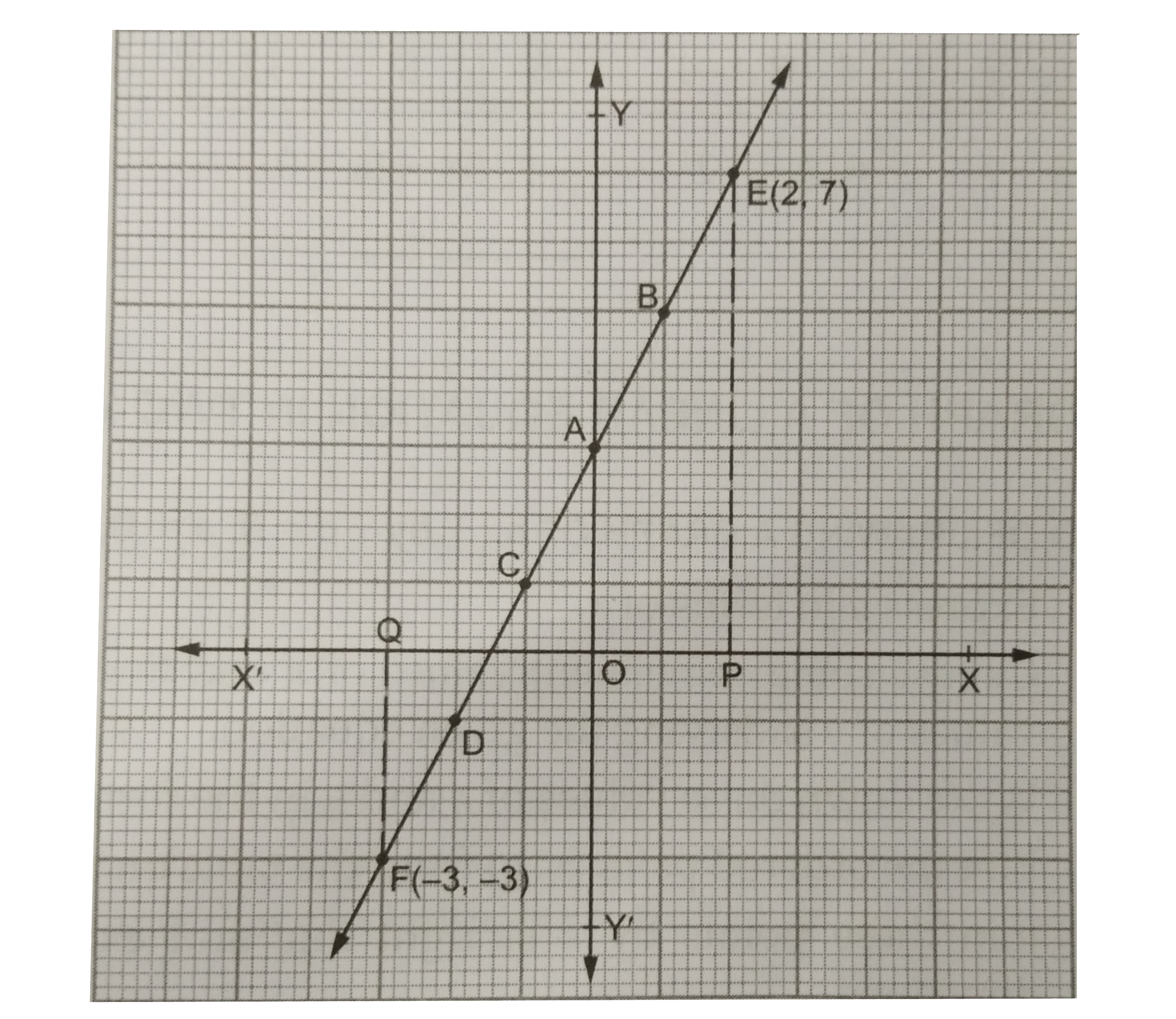



Draw The Graph Of The Equation 2x Y 3 0 Using The Graph Find T



Q Tbn And9gcqnj0vhwe Opg6a9m Kvh Cgzybm58ogx06ggks6qba8vmwvqpx Usqp Cau




Draw The Graph Of Thr Equation 2x 3y 6 0 Brainly In



Draw The Graphs Of The Following Equations 2x 3y 6 0 2x 3y 18 Y 2 0 Sarthaks Econnect Largest Online Education Community




Ex 4 1 Q2 2x Y 6 2x Y 2 0 Solve The Following Equations By Graphical Method



Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Axis Find The Area Of The Shaded Region Sarthaks Econnect Largest Online Education Community




Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Axis Find The Area Brainly In



Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Axis Find The Area Of The Shaded Region Sarthaks Econnect Largest Online Education Community




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper



Solve The System Of Equation By Graphing 2x Y 6 X 2y 2 Mathskey Com




Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Axis Find The Area Brainly In
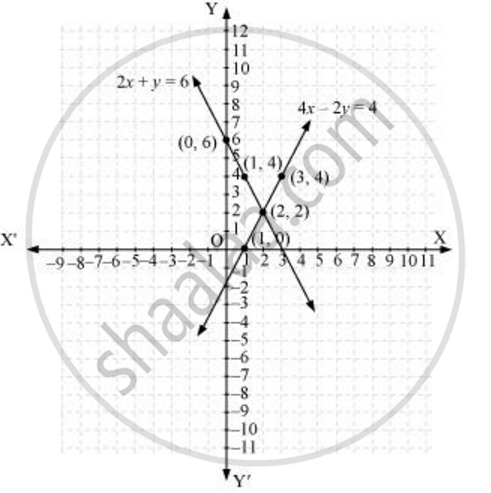



Which Of The Following Pairs Of Linear Equations Are Consistent Inconsistent If Consistent Obtain The Solution Graphically 2x Y 6 0 4x 2y 4 0 Mathematics Shaalaa Com
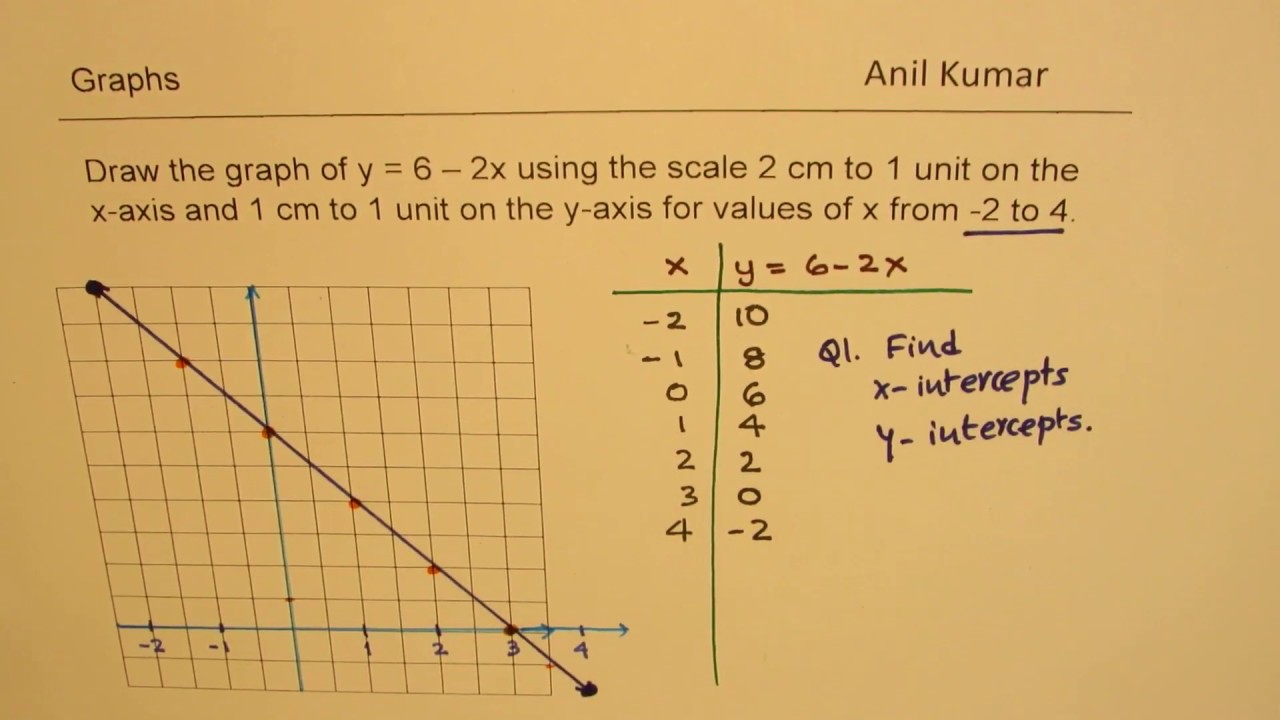



How To Graph Y 6 2x With Given Scale And Domain Youtube




Draw The Graph Of The Following Equations 2x Y 2 0 4x 3y 24 0 Y 4 0 Obtain The Vertices Of The Triangle So Obtained Also Determine Its Area Snapsolve




1 Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Youtube



Q Tbn And9gcqnj0vhwe Opg6a9m Kvh Cgzybm58ogx06ggks6qba8vmwvqpx Usqp Cau




Graphically Solve The Following Pair Of Equations 2x Y 6 2x Y 2 0 Find The Ratio Of The Areas Of The Two Triangles Formed By The




Graphically Solve The Following Pair Of Linear Equation 2x Y 6 And 2x Y 2 0 Find Maths Pair Of Linear Equations In Two Variables Meritnation Com




Ex 6 2 6 Solve 2x 3y 6 Graphically Chapter 6 Class 11




Example 4 Check Whether Equations X 3y 6 And 2x 3y




Ex 6 3 11 Solve 2x Y 4 X Y 3 2x 3y 6




Draw The Graph Of The Equations 2x Y 6 0 And 2x Y 6 0 Also Determine The Coordinates Of The Vertices Of The Triangle Formed By These Lines And The X Axis



How To Find The Equation Of The Line Through The Intersection Of 2x Y 3 0 And 3x Y 7 0 And 2 1 Quora
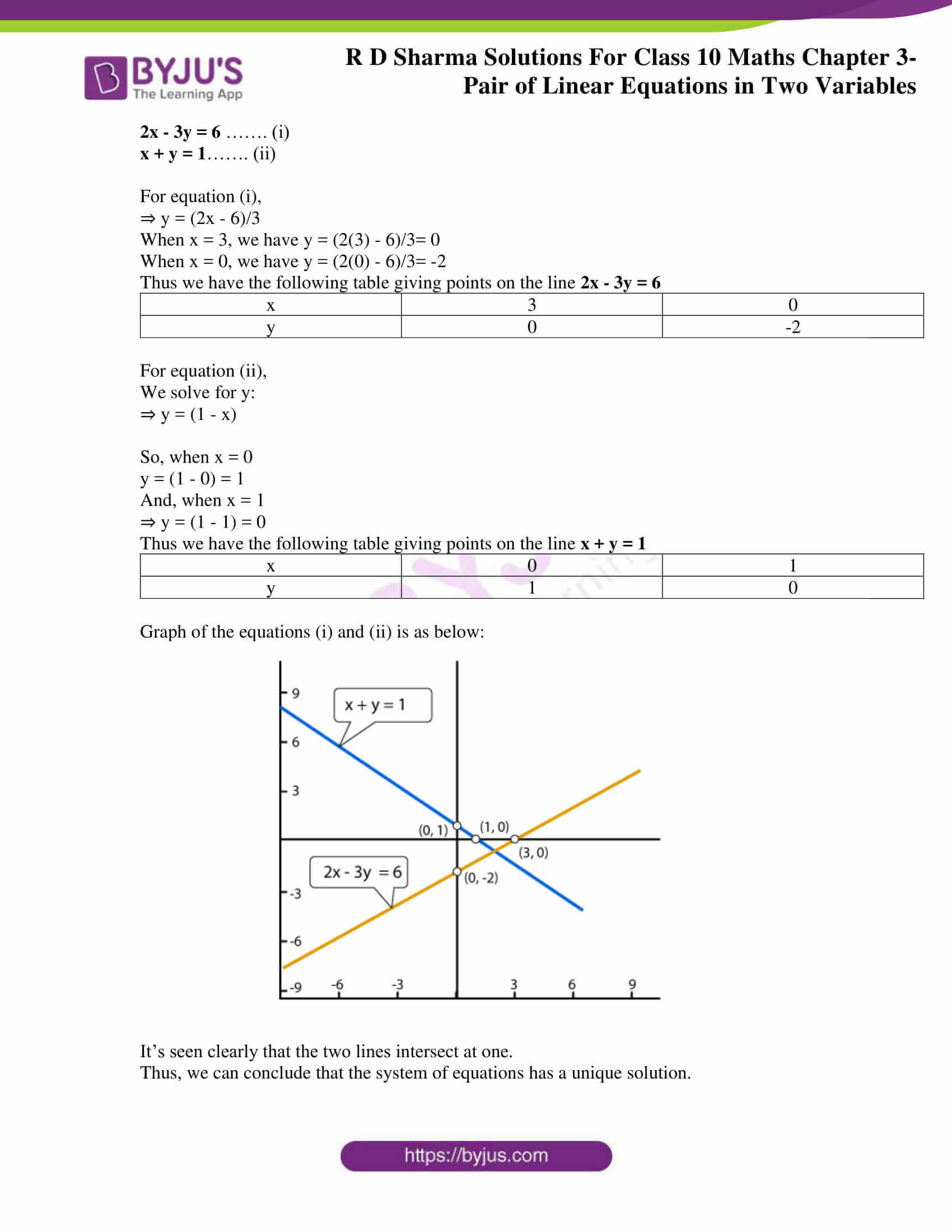



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2



Solution Graph The System Below And Write Its Solution 3x Y 6 Y 1 2x 1



Solution 1 Plot The Graph Of The Equation 2x 3y 6 And 2x Y 10 And Intercept The Result 2 Plot The Graph Of The Equations 2x 4y 10 And 3x 6y 12 And Intercept The Result 3 Determin




G 1 Coaching Class 3rd Chapter Pair Of Linear Equation In Two Variable




Q 38 Graphically Solve The Following Pair Of Equations 2x Y 6 2x Y 2 Maths Coordinate Geometry Meritnation Com




Which Of The Following Pairs Of Linear Equations Are Consistent Inconsistent Consistent Obtain The Solution Graphically 2x Y 6 0 4x 2y 4 0 Own Classes




Draw The Graphs Of The Following Equations 2x 3y 6 0 2x




Draw The Graphs Of The Following Equations 2x Y 2 0 4x 3y 24 0 Y 4 0 Obtain The Verti Youtube




Linear Equation Graph



Q Tbn And9gcse24zlvw1xczpkrqnb9fjgcw0oq1gzd7s3euea Qmpgarm1rrp Usqp Cau




Privado Results



Draw The Graph Of The Following Equation On The Same Graph Paper 2x Y 2 2x Y 6 What Is The Area Of A Trapezium Formed By These Lines Quora
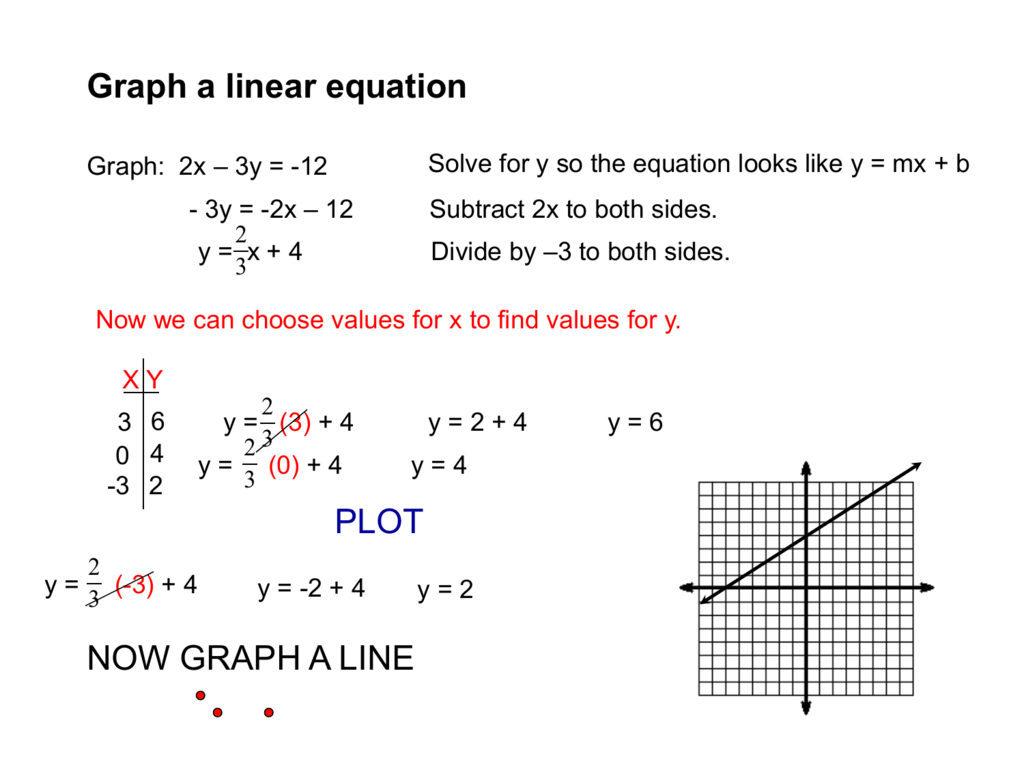



Chapter 7 Powerpoints




Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Y Find The Area Of The Shaded Region




Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Youtube



1




Ex 3 2 Q30 Draw The Graphs Of The Following Equations 2x 3y 6 0 2x 3y 18 0 Y 2 0




Solve The Following System Of Linear Equation Graphically 2x Y 6 0 3x 2y 12 0 Also Find The Vertices Brainly In




Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Youtube




Icise 111 Solve The Following Equations Graphically 1 X 3y 6 2x 3y 12 2 2x Y 6 2x Y 2 0 3 X




Standard Form Examples 3x Y 5 2x Y 10 X Y 6 Ppt Download



Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines And X Axis Find The Area Of The Shaded Region Sarthaks Econnect Largest Online Education Community




Draw The Graphs Of 2x Y 6a N D2x Y 2 0 Shade The Region Boun Ded By These Lines And X Ax Youtube




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Ex 3 A Q15 X 2y 2 0 2x Y 6 0 Solve Each Of The Following Given Systems Of




Writing And Graphing Linear Equations Linear Equations Can
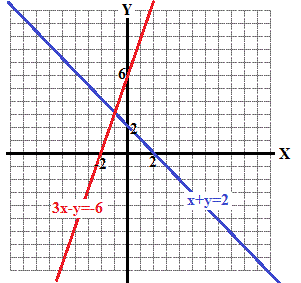



How Do You Solve By Graphing 3x Y 6 And X Y 2 Socratic



Draw The Graph Of 2x Y 6 And 2x Y 2 0 Shade The Region Bounded By These Lines With X Axis Find The Area Of The Shaded Region Mathematics Topperlearning Com p26nrmm




Ex 6 3 3 Solve 2x Y 6 3x 4y 12 Graphically
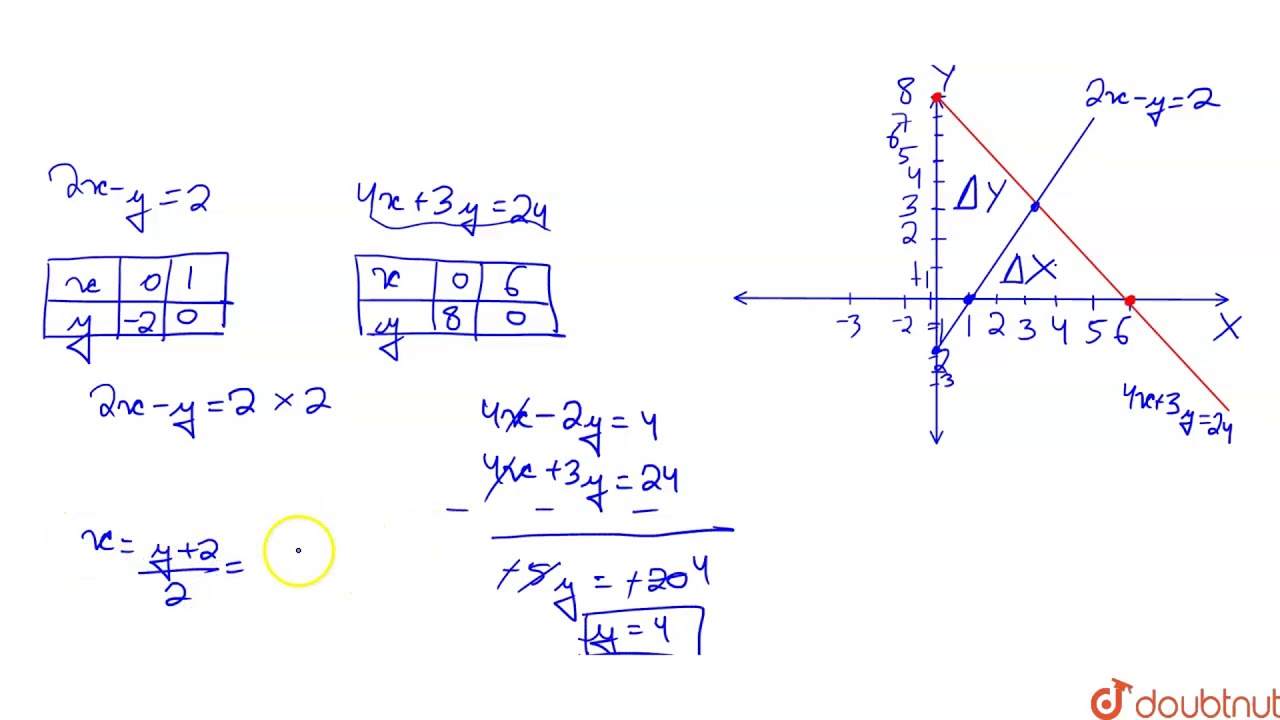



Draw The Graphs Representing The Equations 2x Y 2 And 4x 3y 24 On The Same G Youtube




Draw The Graphs Of The Equations 4x Y 8 0 And 2x 3y 6 0 Also Determine The Vertices Of Brainly In




Solve The Following System Of Linear Equations Graphically 2x Y 6 X 2y 2 0 Find The Area Formed By The Above Two Lines Maths Pair Of Linear Equations In Two Variables Meritnation Com




Ex 6 3 11 Solve 2x Y 4 X Y 3 2x 3y 6




The Graph Of The Linear Equation 2x 3y 6 Cuts The Y Axis At The Point Youtube




Solve Graphically 2x Y 6 Maths Polynomials Meritnation Com




Find The Solution Of The Following Pairs Of Linear Equation By The Graphical Method 2x Y 6 2x Y 2 Brainly In



Solution 2x Y 2 0




Graphically Solve The Following Pair Of Equations 2x Y 6 And
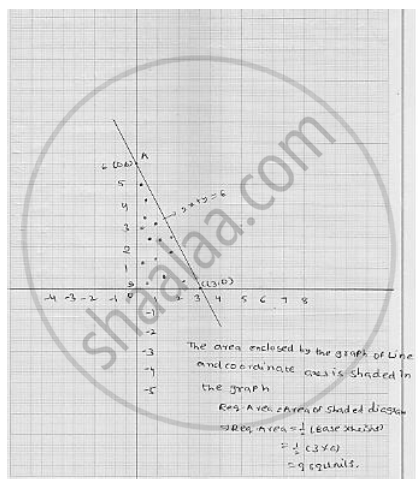



Draw The Graph Of The Equation 2x Y 6 Shade The Region Bounded By The Graph And The Coordinate Axes Also Find The Area Of The Shaded Region Mathematics Shaalaa Com




Ex 6 3 7 Solve 2x Y 8 X 2y 10 Graphically Ex 6 3




Graph Graph Inequalities With Step By Step Math Problem Solver




Graphically Solve The Following Pair Of Equations 2x Y 6 2x Y 2 0 Find The Ratio Of The Areas Of The Two Triangles Formed By The



Systems Of Linear Equations
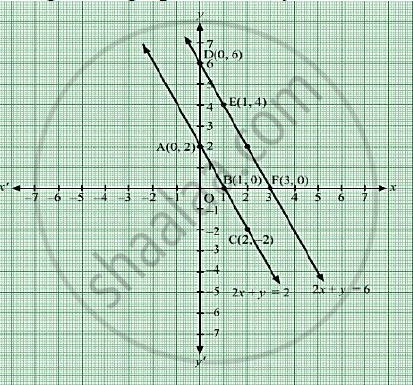



Draw Graphs For Following Equations On The Same Graph Paper 2x Y 2 2x Y 6 Find Co Ordinates Of The Vertices Of Trapezium Formed By These Lines Also




2 Solving A System By Subs Tication U 2 Chegg Com




Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy



0 件のコメント:
コメントを投稿